動(dòng)力系統(tǒng)研究系統(tǒng)的狀態(tài)或性質(zhì)在一套固定規(guī)則下如何更迭變化。當(dāng)系統(tǒng)的初始狀態(tài)與狀態(tài)變化規(guī)則已知,理論上可得之后任一時(shí)刻系統(tǒng)的狀態(tài),但實(shí)際上由于對(duì)初始條件的測(cè)量存在誤差,以及計(jì)算過(guò)程中對(duì)數(shù)值的約算,對(duì)系統(tǒng)狀態(tài)的精準(zhǔn)預(yù)測(cè)被畫(huà)上問(wèn)號(hào)。
 【資料圖】
【資料圖】
本文試著回答以下幾個(gè)問(wèn)題:如何對(duì)動(dòng)力系統(tǒng)進(jìn)行分析?存在不可預(yù)測(cè)的動(dòng)力系統(tǒng)嗎?導(dǎo)致不可預(yù)測(cè)的原因是什么?希望幫助大家對(duì)動(dòng)力系統(tǒng)有更深的理解。
一、戀愛(ài)動(dòng)力學(xué):羅密歐與朱麗葉的愛(ài)恨情仇
高中時(shí)我們都有學(xué)過(guò)導(dǎo)數(shù),對(duì)于:一定不陌生。
表示 R 隨時(shí)間 t 的變化,所以當(dāng)我們知道 f,也就知道了 R 的變化規(guī)則,且該規(guī)則是固定不變的。在這樣的情況下,只要該系統(tǒng)的初始條件已知,理論上我們就能夠利用這個(gè)變化規(guī)則 f 推導(dǎo)出之后任一時(shí)刻的 R。上述過(guò)程就是我們?nèi)シ治觥㈩A(yù)測(cè)一個(gè)動(dòng)力系統(tǒng)的基本思路,但這個(gè)系統(tǒng)是一個(gè)僅包含一個(gè)變量 R 的一維系統(tǒng),并沒(méi)有其他變量與其進(jìn)行交互,所以略顯單調(diào)。
下面我們加入一個(gè)新變量 J 到系統(tǒng)中,給兩個(gè)變量賦予含義,并且讓他們之間產(chǎn)生互動(dòng),從而使我們的系統(tǒng)豐富起來(lái)。
我們假設(shè)此時(shí)愛(ài)可以量化, R 表示羅密歐愛(ài)朱麗葉的程度,J 表示朱麗葉愛(ài)羅密歐的程度,而他們雙方愛(ài)意的變化遵從這個(gè)規(guī)則:
其中 a、d、c、d 為任意常數(shù)。
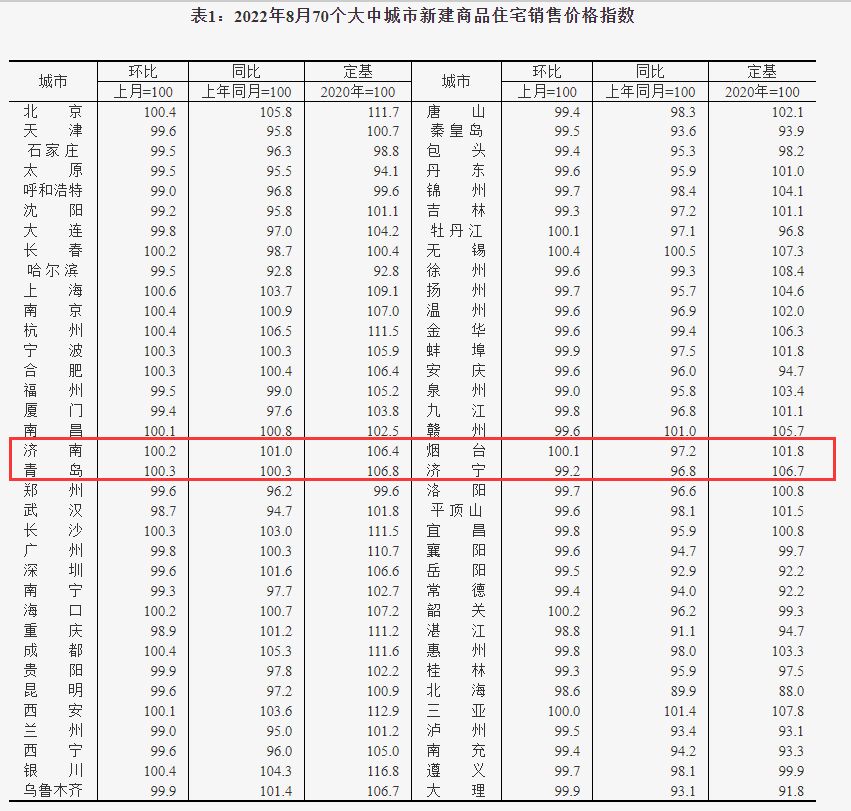
當(dāng) a、d、c、d 取值組合不同,最終會(huì)使得 R 和 J 隨時(shí)間的變化呈現(xiàn)不同的樣態(tài)。比如當(dāng)四個(gè)常數(shù)取值,可以得到羅密歐與朱麗葉的愛(ài)意隨時(shí)間變化的圖像如下圖所示:
根據(jù)圖我們不難發(fā)現(xiàn),在這段關(guān)系中,一方的愛(ài)意大小會(huì)對(duì)另一方的愛(ài)意的變化產(chǎn)生影響,而如何影響是由 a、 d、 c、d 取值決定。針對(duì)上例中取值狀況,我們?nèi)粝脒M(jìn)一步分析二人的愛(ài)意對(duì)對(duì)方的影響,不妨變換坐標(biāo),以 R 為橫軸,J 為縱軸,得到兩人愛(ài)意動(dòng)力系統(tǒng)的相圖:
如何分析該圖呢?我們?nèi)∮疑戏絽^(qū)域放大,按黃色箭頭方向來(lái)看,當(dāng)羅密歐的愛(ài)意上升時(shí),朱麗葉的愛(ài)意會(huì)下降,以同樣的方法去分析另外三個(gè)部分,即可了解二人的愛(ài)意對(duì)對(duì)方的影響。
取不同 a、d、c、d,會(huì)得到不同的雙方愛(ài)意變化規(guī)則,如下圖所示,再根據(jù)二人愛(ài)意的初始值,可得到之后任一時(shí)刻,兩人對(duì)對(duì)方的愛(ài)意數(shù)值,并且根據(jù)兩人愛(ài)意變化的規(guī)則,編出二人間不同的愛(ài)情故事。
上述過(guò)程告訴我們,當(dāng)系統(tǒng)遵循不同的變化規(guī)則,會(huì)使得系統(tǒng)相圖呈現(xiàn)出不同樣態(tài),取不同樣態(tài)間的共性,我們可以將相圖根據(jù)其收斂方向、形態(tài)等特點(diǎn)進(jìn)行分類(lèi),并根據(jù)系統(tǒng)相圖所屬的種類(lèi)的特點(diǎn),對(duì)該系統(tǒng)的發(fā)展有定性了解。
二、混沌:三體運(yùn)動(dòng)不能精確求解
現(xiàn)在,我們?cè)俳o系統(tǒng)內(nèi)加一個(gè)主體,并且讓他們之間存在非線(xiàn)性關(guān)系,也就是變化規(guī)則中存在非線(xiàn)性項(xiàng),這就進(jìn)入到了所謂的 " 三體問(wèn)題 ",事實(shí)上這個(gè)問(wèn)題早在幾百多年前就被提出。
1885 年,在剛創(chuàng)刊不久的瑞典數(shù)學(xué)雜志上出現(xiàn)了一則引人注目的通告:為了慶祝瑞典和挪威國(guó)王奧斯卡二世在 1889 年的六十歲生日,將舉辦一次數(shù)學(xué)比賽,懸賞 2500 克朗和一塊金牌,比賽題目共有四個(gè),其中第一個(gè)就是找到 " 多體問(wèn)題 " 的所有解。而多體問(wèn)題,又可追溯至 17 世紀(jì)晚期,當(dāng)牛頓發(fā)現(xiàn)運(yùn)動(dòng)和引力定律時(shí),牛頓定律非常清晰地闡述了行星軌道的形態(tài)。
乍看上去似乎只要應(yīng)用牛頓定律,就能計(jì)算出任何一組相互間存在引力作用的物體的運(yùn)動(dòng)軌跡,可以是三體、四體或者任意數(shù),只要知道起始狀態(tài),通過(guò)萬(wàn)有引力定律,一定可以把所有物體的任意位移計(jì)算到任意的精確程度。
龐加萊在讀博士期間就已經(jīng)開(kāi)始研究太陽(yáng)系中的多體問(wèn)題,當(dāng)他看到這則通告,毫不猶豫便選擇了這個(gè)問(wèn)題,他進(jìn)展迅速,并完成以任意精度計(jì)算三體的運(yùn)動(dòng)軌跡,雖然這只解決了多體問(wèn)題當(dāng)中的三體情況,但仍征服了評(píng)委,得到這一賽事的獎(jiǎng)勵(lì),且他的解答論文也被刊登在《數(shù)學(xué)學(xué)報(bào)》上。
不幸的是,很快他發(fā)現(xiàn)在證明的關(guān)鍵地方,忽略了數(shù)學(xué)函數(shù)的幾何行為的一種微妙可能性,因此他對(duì)于三體問(wèn)題的解答是錯(cuò)誤的。龐加萊自費(fèi)找回了已經(jīng)被發(fā)放的雜志,并且更改了他的結(jié)論——從微積分的角度而言,萬(wàn)有引力影響下相互作用的三體問(wèn)題沒(méi)有可解析的積分解,這暗示著含有更多數(shù)目的多體問(wèn)題也是無(wú)解的。
以上兩視頻展示了不同初始條件下的三體運(yùn)動(dòng),可以直觀(guān)發(fā)現(xiàn)它們的運(yùn)動(dòng)十分混亂、無(wú)序,且在某時(shí)刻會(huì)因?yàn)橐椆脑虮桓咚購(gòu)楅_(kāi)。若用略為嚴(yán)謹(jǐn)?shù)恼Z(yǔ)言表述其之所以無(wú)法被預(yù)測(cè)的原因,是因?yàn)槊枋鏊鼈兊姆匠虩o(wú)法涵蓋和控制計(jì)算中細(xì)微的不確定性,即任何小數(shù)量級(jí)的誤差都會(huì)導(dǎo)致全然不同的運(yùn)動(dòng)軌跡,這就是混沌的特性。
也正是因此,三體文明才會(huì)選擇對(duì)地球發(fā)起戰(zhàn)爭(zhēng),而不是發(fā)展科技預(yù)測(cè)三顆太陽(yáng)的運(yùn)動(dòng)軌跡,因?yàn)槿魏斡^(guān)測(cè)或是計(jì)算上的微小誤差,會(huì)導(dǎo)出極具差異性的運(yùn)動(dòng)軌跡,也就是摧毀了預(yù)測(cè)的能力。
三、蝴蝶效應(yīng):其實(shí)人家叫 " 對(duì)初始條件的敏感性 " 啦
混沌呈現(xiàn)出系統(tǒng)對(duì)初始條件的敏感性,即同一系統(tǒng),在初始條件有細(xì)微差異的前提下,會(huì)導(dǎo)出兩種完全不同的發(fā)展情況,其實(shí)也就是我們熟知的蝴蝶效應(yīng):一只蝴蝶在巴西扇動(dòng)一下翅膀會(huì)在美國(guó)的得克薩斯州引起一場(chǎng)龍卷風(fēng)。
拿洛倫茲系統(tǒng)來(lái)舉例,如下面的動(dòng)圖所示,即使一開(kāi)始兩個(gè)點(diǎn)相距很近,以至于運(yùn)動(dòng)一段時(shí)間我們都看不出原來(lái)是兩個(gè)點(diǎn),但隨著時(shí)間推移,兩個(gè)點(diǎn)儼然開(kāi)始走起各自的軌道,且兩條軌道毫不相關(guān),唯一的相似之處便是被限制在一定的運(yùn)動(dòng)范圍內(nèi),而這個(gè)是該系統(tǒng)兩個(gè)吸引子的影響。洛倫茲系統(tǒng)遵從的運(yùn)動(dòng)規(guī)則由以下三個(gè)方程決定:
至于如何衡量一個(gè)系統(tǒng)對(duì)初始條件的敏感性,依靠的就是李雅普諾夫指數(shù),它是用來(lái)描述兩個(gè)點(diǎn)相互遠(yuǎn)離的速度。如下圖所示的一個(gè)系統(tǒng)中的兩條軌道:
設(shè)初始時(shí)刻,兩點(diǎn)的距離為,t 時(shí)刻兩點(diǎn)的距離變?yōu)椋覀冊(cè)倭?t 時(shí)刻的距離約等于初始時(shí)刻的距離乘以一個(gè)隨時(shí)間指數(shù)增加的值,即:
其中即為李雅普諾夫指數(shù)。將等號(hào)左右兩邊取對(duì)數(shù),可得如下形式的公式:
我們會(huì)發(fā)現(xiàn)該式的形式與直線(xiàn)的斜截式、相同,所以此時(shí)我們得到的圖將會(huì)成為一條直線(xiàn)。
我們發(fā)現(xiàn)李雅普諾夫指數(shù)就是系統(tǒng)實(shí)際曲線(xiàn)的近似直線(xiàn)的斜率,由此,我們便可以得到系統(tǒng)的李雅普諾夫指數(shù)。
同時(shí),我們?cè)倩氐蕉x李雅普諾夫指數(shù)的公式,會(huì)發(fā)現(xiàn)當(dāng)其為正時(shí),因
為一定值,故會(huì)以指數(shù)速度增加,換言之,系統(tǒng)中兩點(diǎn)會(huì)以指數(shù)速度分離,也就是進(jìn)入兩條毫不相關(guān)的軌道。
而對(duì)于系統(tǒng)是否存在動(dòng)力學(xué)混沌,可以從最大李雅普諾夫指數(shù)是否大于零非常直觀(guān)地進(jìn)行判斷——正李雅普諾夫指數(shù),意味著在系統(tǒng)相空間中,無(wú)論初始時(shí)刻兩點(diǎn)距離多么靠近,其間距都會(huì)隨著時(shí)間成指數(shù)率的增加以致達(dá)到無(wú)法預(yù)測(cè),這也就是我們所說(shuō)的混沌現(xiàn)象,而李雅普諾夫指數(shù)的大小,暗示著兩點(diǎn)分開(kāi)的速度,也就是系統(tǒng)進(jìn)入混沌狀態(tài)的速度,或者也可以說(shuō)系統(tǒng)不再能被預(yù)測(cè)的速度。
此時(shí)再回過(guò)頭去看一些系統(tǒng),根據(jù)其李雅普諾夫指數(shù)的大小,我們便能大致估計(jì)出對(duì)系統(tǒng)進(jìn)行預(yù)測(cè)的程度。例如對(duì)于太陽(yáng)系各行星運(yùn)動(dòng),我們能預(yù)測(cè)到 400~500 萬(wàn)年左右,對(duì)于天氣系統(tǒng),我們能預(yù)測(cè)到 15 天左右,而對(duì)于混沌電路,則僅能預(yù)測(cè) 1 毫秒左右。
因此由于系統(tǒng)的非線(xiàn)性性質(zhì),部分系統(tǒng)將面臨必然走向混沌的結(jié)果,故而我們不能僅通過(guò)觀(guān)測(cè)其在某一時(shí)刻的狀態(tài)與演化規(guī)律,就精確預(yù)測(cè)任意時(shí)刻后該系統(tǒng)的狀態(tài)。因此,就無(wú)須抱有一些不切實(shí)際的期待,比如希望天氣預(yù)報(bào)給出未來(lái)一個(gè)月的天氣情況。
四、對(duì)于混沌的最新研究
正如前文所講,多數(shù)非線(xiàn)性系統(tǒng)難以求解析解,因?yàn)橄噍^于線(xiàn)性系統(tǒng),它不能分成幾個(gè)部分單獨(dú)求解,并重新整合。但自然界的很多復(fù)雜系統(tǒng),如氣象變化、化學(xué)反應(yīng)、病毒感染、人口移動(dòng)、社會(huì)行為等,各部分會(huì)相互影響、合作或競(jìng)爭(zhēng),也就是出現(xiàn)很多非線(xiàn)性作用,因此學(xué)會(huì)用整體的目光,關(guān)注系統(tǒng)中的復(fù)雜性與偶然性就顯得尤為重要。
混沌理論就是非線(xiàn)性科學(xué)中發(fā)展出的理論,它是關(guān)于系統(tǒng)從有序突然變?yōu)闊o(wú)序狀態(tài)的一種演化理論,是對(duì)不規(guī)則而又無(wú)法預(yù)測(cè)的現(xiàn)象及其過(guò)程的分析。
然而,混沌不是純粹的無(wú)序,而是不具備周期性變化和其他明顯對(duì)稱(chēng)特征的有序態(tài),因此該理論可以為我們研究自然科學(xué)或社會(huì)科學(xué)中諸多現(xiàn)象的不確定性做出解釋與分析。與此同時(shí),該理論延展出的如何控制或利用混沌現(xiàn)象的研究,還被應(yīng)用于神經(jīng)網(wǎng)絡(luò)、非線(xiàn)性電路、天體力學(xué)、非線(xiàn)性機(jī)械故障診斷系統(tǒng)等諸多領(lǐng)域,向我們展示了其廣闊的發(fā)展前景。
本文內(nèi)容整理自北京師范大學(xué)復(fù)雜系統(tǒng)國(guó)際科學(xué)中心劉宇老師的直播:動(dòng)力系統(tǒng)分析:" 三體 " 運(yùn)動(dòng)為什么不能精確預(yù)測(cè)?本文來(lái)自微信公眾號(hào):集智俱樂(lè)部 (ID:swarma_org),作者:劉宇,整理:董佳欣,編輯:鄧一雪,原文標(biāo)題:《如何預(yù)測(cè)混沌?從羅密歐與朱麗葉的戀愛(ài)動(dòng)力學(xué),到三體問(wèn)題》
-
當(dāng)前速訊:國(guó)家衛(wèi)健委:昨日新增本土“3041+29654”
頭條 22-11-25
-
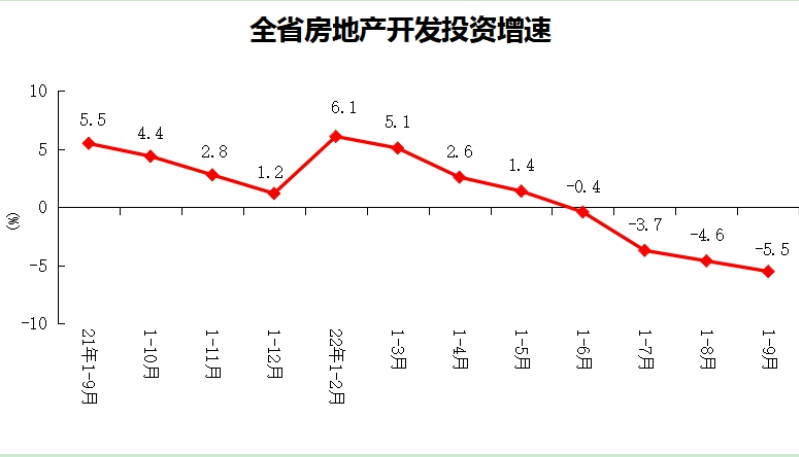
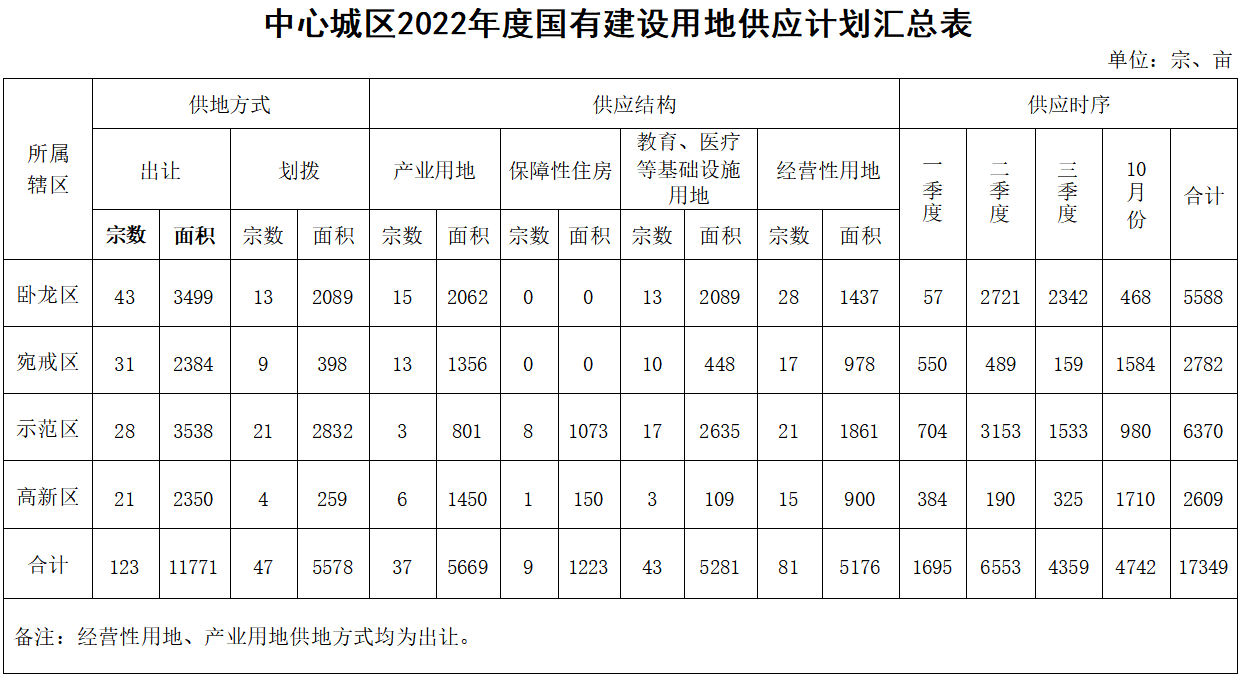
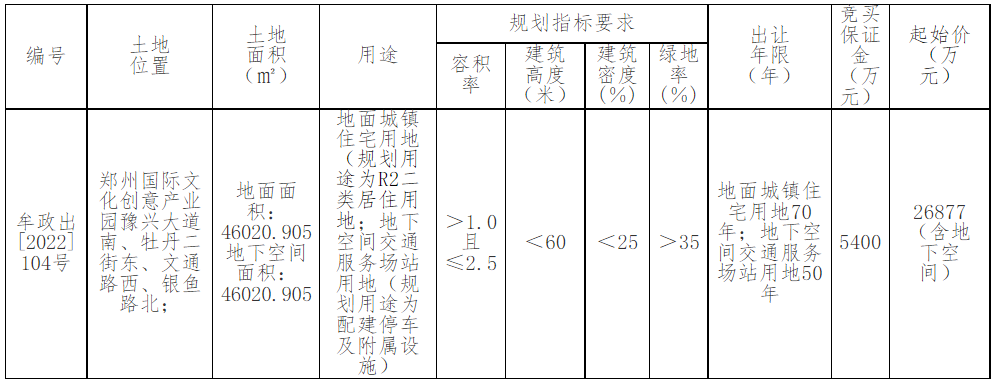
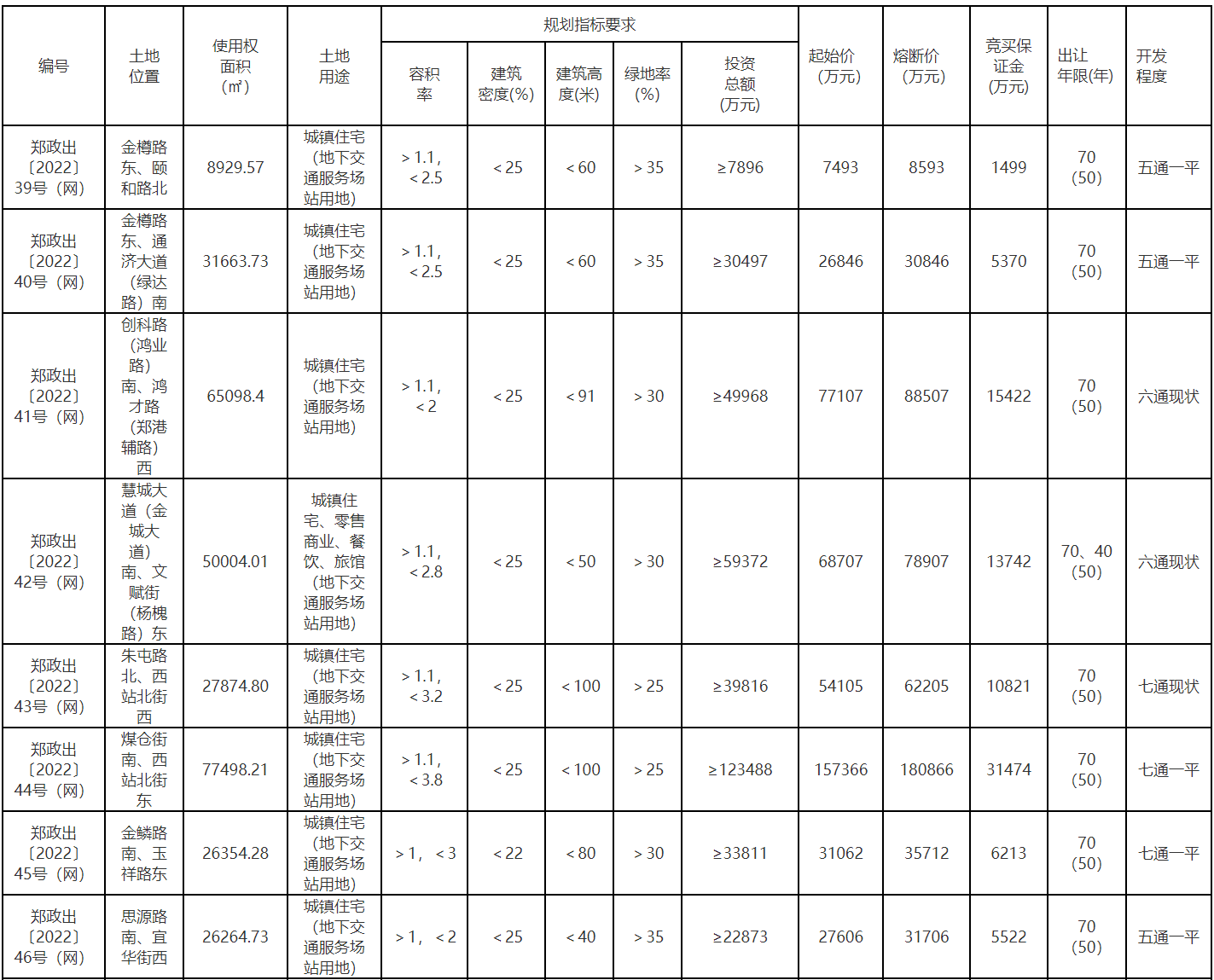
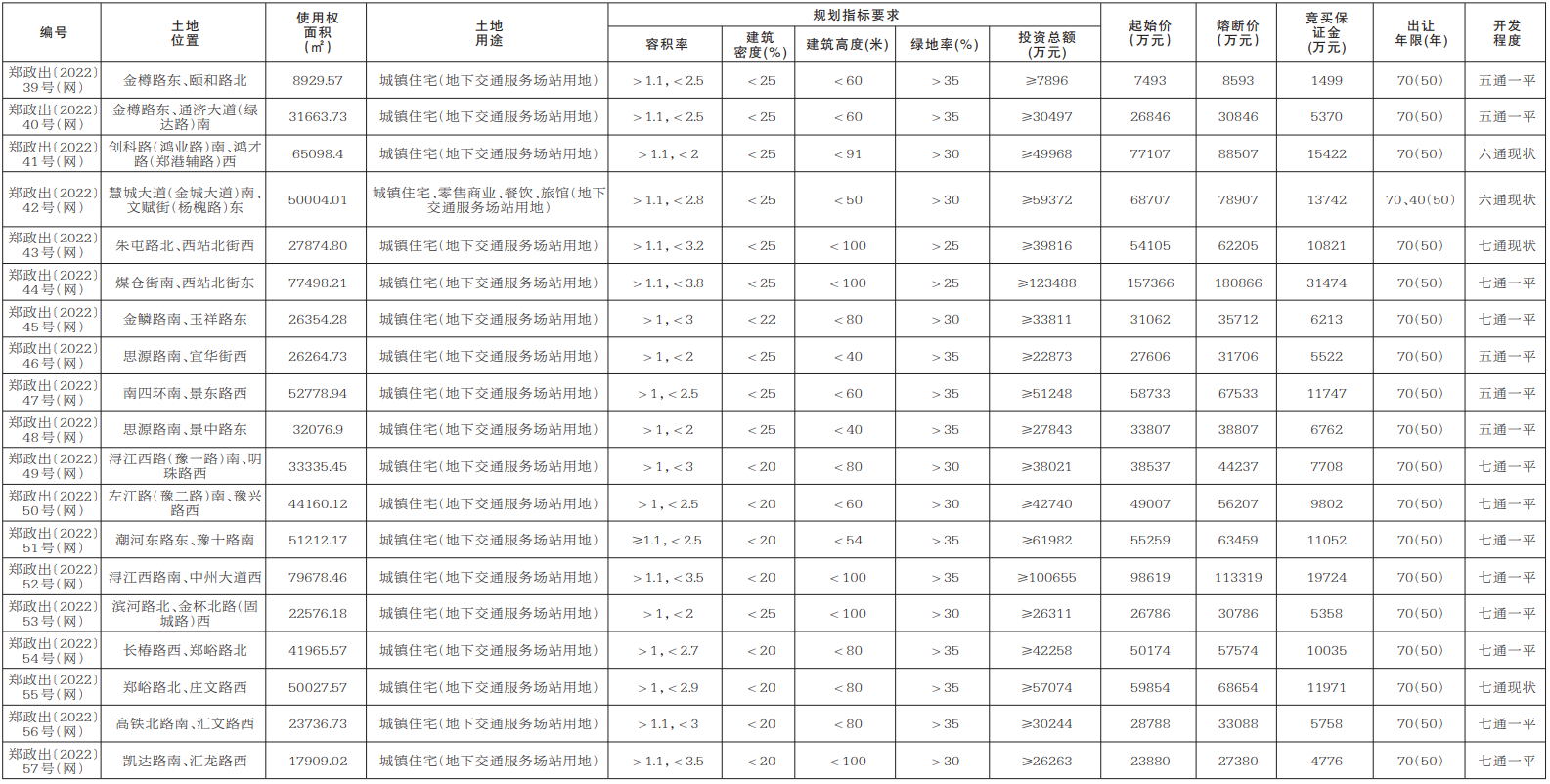
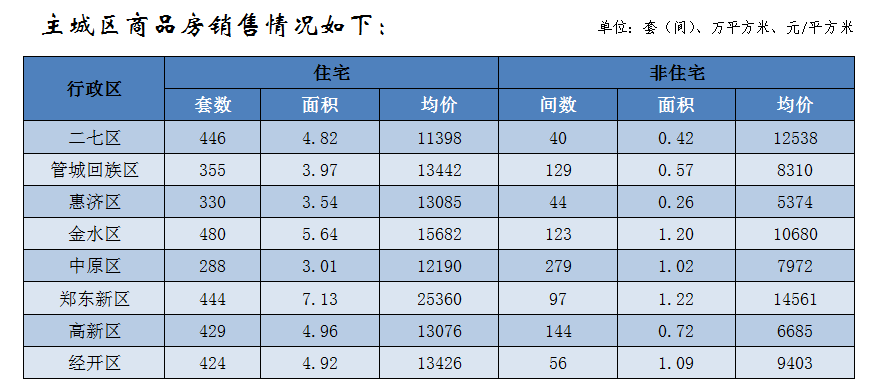
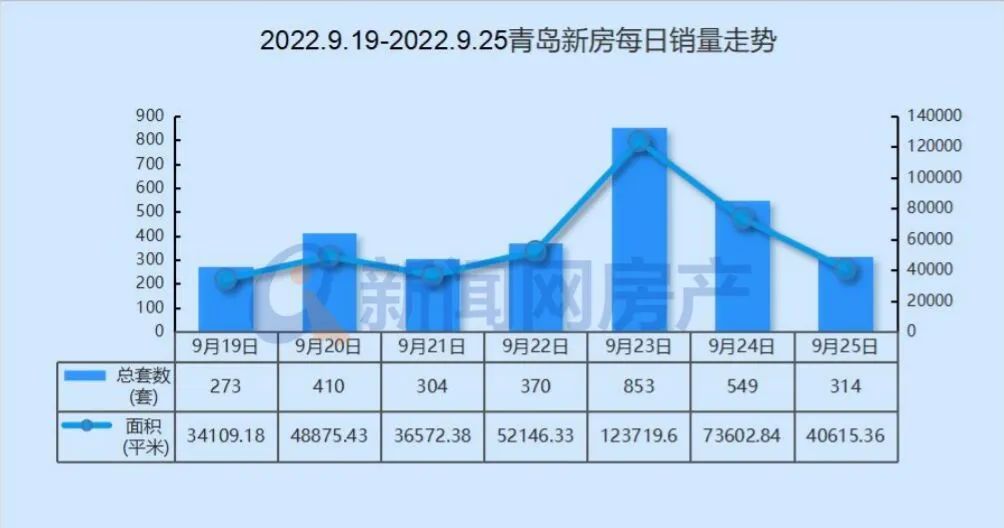
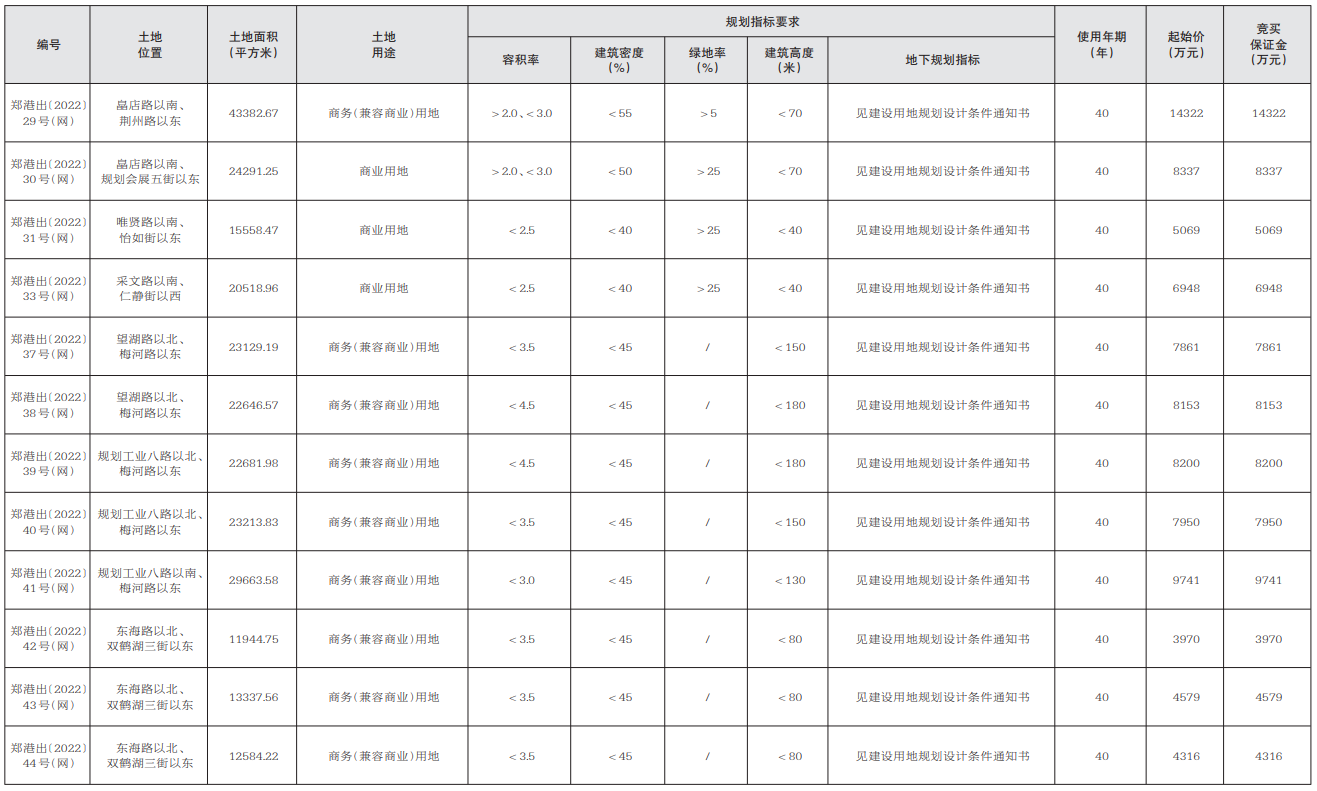
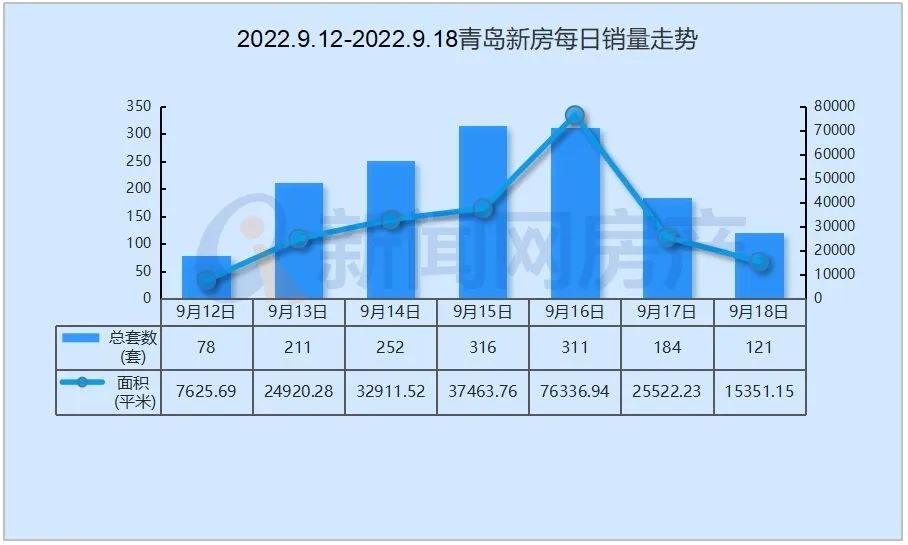
【天天時(shí)快訊】成交額4.87億元,鄭州4宗164畝土地完成出讓
頭條 22-11-25
-
恒大突發(fā)!11宗地遭政府無(wú)償收回,凈用地面積2071.3畝!什么情況?
頭條 22-11-25
-
河南昨日新增本土感染140+719
頭條 22-11-25
-
【環(huán)球新要聞】起始價(jià)9.97億元!鄭州5宗零售商業(yè)用地掛牌出讓
頭條 22-11-25
-
隔夜歐美·11月25日
頭條 22-11-25
-
焦點(diǎn)要聞:鄭州高新區(qū)新增9個(gè)高風(fēng)險(xiǎn)區(qū)
頭條 22-11-25
-
全球視點(diǎn)!立方風(fēng)控鳥(niǎo)·早報(bào)(11月25日)
頭條 22-11-25
-
【新要聞】鄭州市金水區(qū)解除一處高風(fēng)險(xiǎn)臨時(shí)管控區(qū)
頭條 22-11-25
-
“第二支箭”增信首批民營(yíng)房企債券發(fā)行
頭條 22-11-24
-
世界信息:辟謠!網(wǎng)傳南陽(yáng)市將封城系謠言
頭條 22-11-24
-
鄭州開(kāi)放142處核酸采樣屋,方便保供等重點(diǎn)人員核酸檢測(cè)
頭條 22-11-24
-
今日訊!登封市通告:14個(gè)區(qū)域劃定為高風(fēng)險(xiǎn)區(qū)
頭條 22-11-24
-
鄭州明日零點(diǎn)再啟“防疫攻堅(jiān)” 市民買(mǎi)菜儲(chǔ)糧高潮已退
頭條 22-11-24
-
每日熱點(diǎn):立方風(fēng)控鳥(niǎo)·晚報(bào)(11月24日)
頭條 22-11-24
-
碧桂園獲三家國(guó)有大行授信支持 總額度超1500億元
頭條 22-11-24
-
助農(nóng)蔬菜進(jìn)鄭州,通行證怎么辦?保供證明怎么開(kāi)?答案都在這里
頭條 22-11-24
-
觀(guān)天下!中央網(wǎng)信辦公布第三批首發(fā)謠言典型案例
頭條 22-11-24
-
美的置業(yè)獲四家國(guó)有大行授信支持
頭條 22-11-24
-
環(huán)球速讀:鄭州銀行:行長(zhǎng)趙飛任職資格獲核準(zhǔn)
頭條 22-11-24
-
鄭州銀行擬發(fā)行50億元金融債,債券評(píng)級(jí)AAA
頭條 22-11-24
-
世界視訊!彭波一審獲刑14年 非法收受5464萬(wàn)余元
頭條 22-11-24
-
環(huán)球微資訊!東航、南航擬發(fā)行共35億元超短融,用于償還債務(wù)等
頭條 22-11-24
-
劉忻、張雁云任浙江省副省長(zhǎng)
頭條 22-11-24
-
天天頭條:鄭州市科技局公示6家高新技術(shù)企業(yè)受理補(bǔ)充名單
頭條 22-11-24
-
天天快資訊丨河南省開(kāi)展信用提升行動(dòng) 助力市場(chǎng)主體紓困解難
頭條 22-11-24
-
世界熱推薦:河南全力保障疫情期間群眾緊急就醫(yī)需求六項(xiàng)規(guī)定
頭條 22-11-24
-
河南昨日新增本土確診病例159例,無(wú)癥狀感染者536例
頭條 22-11-24
-
環(huán)球視訊!河南省國(guó)家物流樞紐增至6個(gè) 居全國(guó)第一
頭條 22-11-24

- 全球視點(diǎn)!“三體”運(yùn)動(dòng)為什么不能精確預(yù)測(cè)2022-12-04
- 30 系顯卡清倉(cāng)大促!RTX3070 破發(fā)了2022-12-04
- 機(jī)頂盒大小!小米首款 NUC 桌面迷你機(jī)將2022-12-04
- 必買(mǎi):70 寸 4K 電視跌破 2000 這幾款2022-12-04
- 熱議:拉薩市12月4日起逐步恢復(fù)城市公交運(yùn)營(yíng)2022-12-04
- 腫瘤醫(yī)院因?yàn)殛?yáng)性停診?癌癥治療不比新冠更2022-12-04
- 全球熱門(mén):鄭州機(jī)場(chǎng)客運(yùn)航班快速恢復(fù) 南飛2022-12-04
- 努力工作卻不被喜歡,多數(shù)是這五個(gè)原因,早2022-12-04
- 經(jīng)開(kāi)區(qū)原心 綠色科技 + 微度假人居2022-12-04
- 馬斯克年末爆大瓜!爆拜登之子黃毒丑聞,扒2022-12-04
- 環(huán)球動(dòng)態(tài):廣州昨日新增 4581 例新冠病毒2022-12-04
- 鄭州機(jī)場(chǎng)客運(yùn)航班快速恢復(fù) 南飛航班成領(lǐng)頭2022-12-04
- “垃圾佬” Up 主上手 Intel 酷睿 i5-2022-12-04
- 世界今日?qǐng)?bào)丨12 月 3 日 0 時(shí)至 24 2022-12-04
- 世界熱門(mén):強(qiáng)強(qiáng)聯(lián)手!保利 · 和院 & 中2022-12-04
- 天天視點(diǎn)!“洗衣液中的愛(ài)馬仕”召回 5932022-12-04
- 即時(shí)看!武大院士為湖工商大學(xué)生講解“智能2022-12-04
- 信息:特約評(píng)論員錢(qián)亮丨勞塔羅,盧卡庫(kù)附體2022-12-04
- 世界實(shí)時(shí):12月5日!龍門(mén)石窟景區(qū)將恢復(fù)開(kāi)園2022-12-04
- 世界速遞!俄烏沖突將放緩?美情報(bào)部門(mén)最新2022-12-04
- 最新快訊!12 月 3 日廣州新增感染者詳情2022-12-04
- 天天即時(shí):錯(cuò)誤佩戴隱形眼鏡,或致失明!這2022-12-04
- 一年兩次出手救同一人!金圣榆,謝謝你!2022-12-04
- 環(huán)球短訊!航天新征程 | 神舟十四號(hào)載人2022-12-04
- 即時(shí)焦點(diǎn):阿布洛哈村:大山深處的“幸福路2022-12-04
- 大象幫·小新疫線(xiàn)問(wèn)答丨疫情之下,家里常備2022-12-04
- 環(huán)球動(dòng)態(tài):上海:市內(nèi)公共交通、室外公共場(chǎng)2022-12-04
- 環(huán)球快消息!央行、證監(jiān)會(huì)公告:12月6日上2022-12-04
- 以古為基 以技為翼|十八數(shù)藏在元宇宙時(shí)代2022-12-04
- 天天滾動(dòng):@鄭州人,你今天做上核酸了嗎?2022-12-04
精彩推薦
閱讀排行
- 鄭州機(jī)場(chǎng)客運(yùn)航班快速恢復(fù) 南飛航班成領(lǐng)頭雁
- 信息:特約評(píng)論員錢(qián)亮丨勞塔羅,盧卡庫(kù)附體
- 世界實(shí)時(shí):12月5日!龍門(mén)石窟景區(qū)將恢復(fù)開(kāi)園
- 大象幫·小新疫線(xiàn)問(wèn)答丨疫情之下,家里常備哪些藥?
- 天天滾動(dòng):@鄭州人,你今天做上核酸了嗎?
- 速訊:河南疾控發(fā)布重要提醒
- 【全球獨(dú)家】特約評(píng)論|范大廚是個(gè)好廚師
- 12月3日河南新增本土“86+264”
- 最新:息縣數(shù)百萬(wàn)斤蘿卜愛(ài)心促銷(xiāo)進(jìn)行中
- 當(dāng)前信息:12月9日,銀基國(guó)際旅游度假區(qū)恢復(fù)開(kāi)放!